Maximizing earns or minimizing losses has always been a concern in engineering problems. For diverse fields of knowledge, the complexity of optimization problems increases as science and technology develop. Often, examples of engineering problems that might require an optimization approach are in energy conversion and distribution, in mechanical design, in logistics, and in the reload of nuclear reactors.

To maximize or minimize a function in order to find the optimum, there are several approaches that one could perform. In spite of a wide range of optimization algorithms that could be used, there is not a main one that is considered to be the best for any case. One optimization method that is suitable for a problem might not be so for another one; it depends on several features, for example, whether the function is differentiable and its concavity (convex or concave). In order to solve a problem, one must understand different optimization methods so this person is able to select the algorithm that best fits on the features’ problem.

The particle swarm optimization (PSO) algorithm, proposed by Kennedy and Eberhart , is a metaheuristic algorithm based on the concept of swarm intelligence capable of solving complex mathematics problems existing in engineering . It is of great importance noting that dealing with PSO has some advantages when compared with other optimization algorithms, once it has fewer parameters to adjust, and the ones that must be set are widely discussed in the literature.

In the early of 1990s, several studies regarding the social behavior of animal groups were developed. These studies showed that some animals belonging to a certain group, that is, birds and fishes, are able to share information among their group , and such capability confers these animals a great survival advantage. Inspired by these works, Kennedy and Eberhart proposed in 1995 the PSO algorithm , a metaheuristic algorithm that is appropriate to optimize nonlinear continuous functions. The author derived the algorithm inspired by the concept of swarm intelligence, often seen in animal groups, such as flocks and shoals.

In order to explain how the PSO had inspired the formulation of an optimization algorithm to solve complex mathematical problems, a discussion on the behavior of a flock is presented. A swarm of birds flying over a place must find a point to land and, in this case, the definition of which point the whole swarm should land is a complex problem, since it depends on several issues, that is, maximizing the availability of food and minimizing the risk of existence of predators. In this context, one can understand the movement of the birds as a choreography; the birds synchronically move for a period until the best place to land is defined and all the flock lands at once.

In the given example, the movement of the flock only happens as described once all the swarm members are able to share information among themselves; otherwise, each animal would most likely land at a different point and at a different time. The studies regarding the social behavior of animals from the early 1990s stated before in this text pointed out that all birds of a swarm searching for a good point to land are able to know the best point until it is found by one of the swarm’s members. By means of that, each member of the swarm balances its individual and its swarm knowledge experience, known as social knowledge. One may notice that the criteria to assess whether a point is good or not in this case is the survivalconditions found at a possible landing point, such as those mentioned earlier in this text.

The problem to find the best point to land described features an optimization problem. The flock must identify the best point, for example, the latitude and the longitude, in order to maximize the survival conditions of its members. To do so, each bird flies searching and assessing different points using several surviving criteria at the same time. Each one of those has the advantage to know where the best location point is found until known by the whole swarm.

The goal of an optimization problem is to determine a variable represented by a vector X=[x1x2x3…xn]X=x1x2x3…xn that minimizes or maximizes depending on the proposed optimization formulation of the function f(X). The variable vector XX is known as position vector; this vector represents a variable model and it is nn dimensions vector, where nn represents the number of variables that may be determined in a problem, that is, the latitude and the longitude in the problem of determining a point to land by a flock. On the other hand, the function f(X) is called fitness function or objective function, which is a function that may assess how good or bad a position XX is, that is, how good a certain landing point a bird thinks it is after this animal finds it, and such evaluation in this case is performed through several survival criteria.

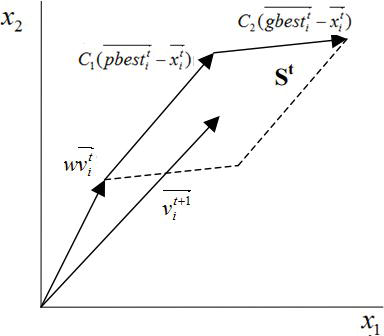
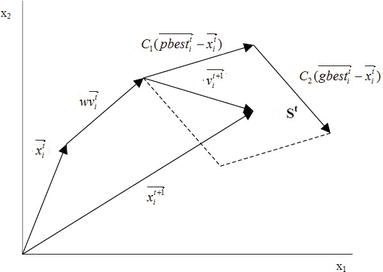
Considering a swarm with P particles, there is a position vector Xti=(xi1xi2xi3…xin)TXit=xi1xi2xi3…xinT and a velocity vector Vti=(vi1vi2vi3…vin)TVit=vi1vi2vi3…vinT at a t iteration for each one of the i particle that composes it. These vectors are updated through the dimension j according to the following equations:

Vt+1ij=wVtij+c1rt1(pbestij−Xtij)+c2rt2(gbestj−Xtij)Vijt+1=wVijt+c1r1tpbestij−Xijt+c2r2tgbestj−XijtE1

and

Xt+1ij=Xtij+Vt+1ijXijt+1=Xijt+Vijt+1

where i = 1,2,…,P and j = 1,2,…,n.

Eq. (1) denotes that there are three different contributions to a particle’s movement in an iteration, so there are three terms in it that are going to be further discussed. Meanwhile, Eq. (2) updates the particle’s positions. The parameter ww is the inertia weight constant, and for the classical PSO version, it is a positive constant value. This parameter is important for balancing the global search, also known as exploration (when higher values are set), and local search, known as exploitation (when lower values are set). In terms of this parameter, one may notice that it is one of the main differences between classical version of PSO and other versions derived from it.

Velocity update equation’s first term is a product between parameter w and particle’s previous velocity, which is the reason it denotes a particles’ previous motion into the current one. Hence, for example, if w=1w=1, the particle’s motion is fully influenced by its previous motion, so the particle may keep going in the same direction. On the other hand, if 0≤w<10≤w<1, such influence is reduced, which means that a particle rather goes to other regions in the search domain. Therefore, as the inertia weight parameter is reduced, the swarm may explore more areas in the searching domain, which means that the chances of finding a global optimum may increase. However, there is a price when using lower w values, which is the simulations turn out to be more time consuming [1].

The individual cognition term, which is the second term of Eq. (1), is calculated by means of the difference between the particle’s own best position, for example, pbestijpbestij, and its current position XtijXijt. One may notice that the idea behind this term is that as the particle gets more distant from the pbestijpbestij position, the difference (pbestij−Xtij)pbestij−Xijt must increase; therefore, this term increases, attracting the particle to its best own position. The parameter c1c1 existing as a product in this term is a positive constant and it is an individual-cognition parameter, and it weighs the importance of particle’s own previous experiences. The other parameter that composes the product of second term is r1r1, and this is a random value parameter with [0,1]01 range. This random parameter plays an important role, as it avoids premature convergences, increasing the most likely global optima [1].

Finally, the third term is the social learning one. Because of it, all particles in the swarm are able to share the information of the best point achieved regardless of which particle had found it, for example, gbestjgbestj. Its format is just like the second term, the one regarding the individual learning. Thus, the difference (gbestj−Xtij)gbestj−Xijt acts as an attraction for the particles to the best point until found at some tt iteration. Similarly, c2c2 is a social learning parameter, and it weighs the importance of the global learning of the swarm. And r2r2 plays exactly the same role as r1r1.

Lastly, Figure 1 shows the PSO algorithm flowchart, and one may notice that the optimization logic in it searches for minimums and all position vectors are assessed by the function f(X)fX, known as fitness function. Besides that, Figures 2 and 3 present the update in a particle’s velocity and in its position at a tt iteration, regarding a bi-dimensional problem with variables x1x1 and x2.